The Square Root Of Twenty-Five: A Mathematical Journey

The Square Root of Twenty-Five: A Mathematical Journey

Related Articles: The Square Root of Twenty-Five: A Mathematical Journey

• DV Lottery 2025 Application Form: A Comprehensive Guide
• How Many Days Until January 20, 2025? A Comprehensive Timeline And Countdown
• Near Protocol Price Prediction 2024: A Comprehensive Analysis
• Vanguard Target Retirement 2025 Inst: A Comprehensive Guide
• 2025 Lexus ES 350 F Sport: A Symphony Of Luxury And Performance

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Square Root of Twenty-Five: A Mathematical Journey. Let’s weave interesting information and offer fresh perspectives to the readers.

Video about The Square Root of Twenty-Five: A Mathematical Journey

The Square Root of Twenty-Five: A Mathematical Journey

In the realm of mathematics, the square root of a number holds a significant position. It represents the inverse operation of squaring, revealing the value that, when multiplied by itself, yields the original number. In this article, we embark on a mathematical odyssey to explore the square root of twenty-five, a number that unveils intriguing properties and applications.

Defining the Square Root

The square root of a number is the value that, when multiplied by itself, produces the original number. Symbolically, it is represented as √x, where x is the number under consideration. For instance, the square root of nine is three, denoted as √9 = 3, since 3 × 3 = 9.

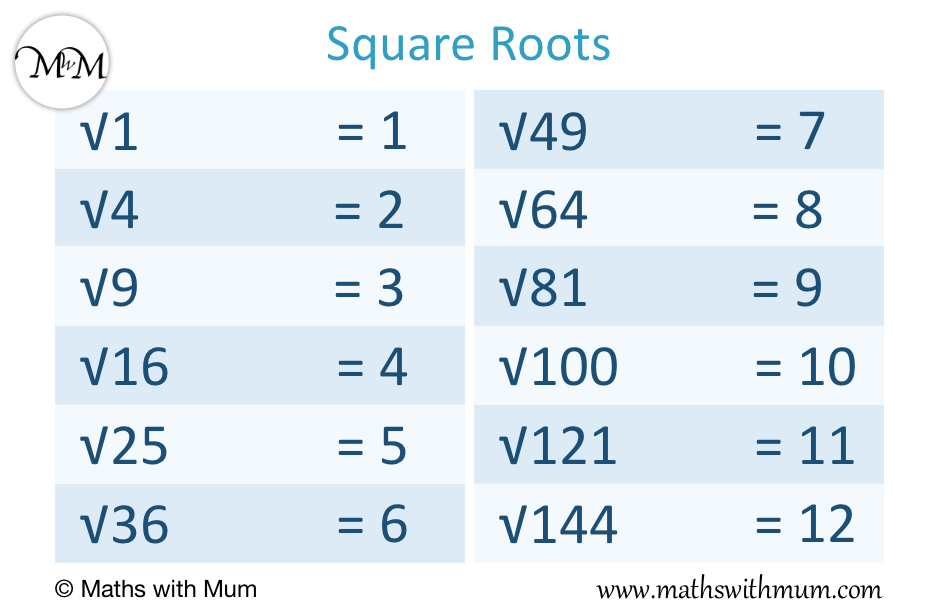
The Square Root of Twenty-Five

Applying this concept to our subject of interest, the square root of twenty-five is the value that, when squared, equals twenty-five. This value is five, as 5 × 5 = 25. Therefore, we can express this mathematically as √25 = 5.

Properties of the Square Root of Twenty-Five

The square root of twenty-five possesses several noteworthy properties:

1. Positive Value: The square root of a positive number is always positive. Therefore, √25 = 5, and not -5.

2. Irrational Number: The square root of twenty-five is an irrational number, meaning it cannot be expressed as a fraction of two integers. It is a non-terminating, non-repeating decimal.

3. Real Number: Despite being irrational, the square root of twenty-five is a real number, lying on the real number line.

Applications of the Square Root of Twenty-Five

The square root of twenty-five finds applications in various fields, including:

1. Geometry: In geometry, the square root of twenty-five is used to calculate the diagonal of a square with sides of length five units. The diagonal’s length is given by √25 = 5 units.

2. Trigonometry: In trigonometry, the square root of twenty-five is used to determine the sine and cosine of 45 degrees. Both sine and cosine of 45 degrees are equal to √25/25 = 1/√2.

3. Physics: In physics, the square root of twenty-five is used to calculate the speed of an object in a uniform circular motion. The formula involves √25, which represents the object’s centripetal acceleration.

Historical Significance

The square root of twenty-five has been studied and used throughout history. Ancient mathematicians, such as the Babylonians and Greeks, developed methods to approximate its value. The symbol √, denoting the square root, was introduced by the Arab mathematician al-Khwarizmi in the 9th century.

Conclusion

The square root of twenty-five, a seemingly simple concept, reveals a wealth of mathematical properties and applications. It is a positive, irrational, and real number that plays a role in various fields, from geometry to physics. Understanding the square root of twenty-five not only enhances our mathematical knowledge but also provides a glimpse into the fascinating world of mathematics.

Closure

Thus, we hope this article has provided valuable insights into The Square Root of Twenty-Five: A Mathematical Journey. We appreciate your attention to our article. See you in our next article!